二叉树的遍历前序中序后序分别实现递归和非递归遍历方式

BinaryTree.h

#ifndef _BINARY_TREE_H_
#define _BINARY_TREE_H_
#include <string>
 
typedef int POS;
typedef int METHOD;
typedef std::string String;
 
enum { LeftChild, RightChild };
enum { Preorder, Inorder, Postorder };
 
struct Node
{
 String elem;
 Node* left;
 Node* right;
 
 Node() { elem = ""; left = right = NULL; }
 Node(const String& str) { elem = str; left = right = NULL; }
};
 
class BinaryTree
{
public:
 BinaryTree(void);
 ~BinaryTree(void);
 
public:
 //@ DESC：输出树
 //\params: 
 // method, 为 中序后序前序三种遍历方式，
 // recursive, 为是否使用递归的方式
 void     DumpTree( METHOD method, bool recursive = false );
 //@ DESC：创建一棵树，其实就是初始化了根节点
 //\params:  
 // rootContent, 参见Node的定义，其中elem的类型为std::string, 其实就是为了传入根节点的内容
 void     CreateTree( const String& rootContent );
 //@ DESC：插入一个节点
 //\params:
 // root, 参数node的父节点
 // node, 要插入的节点
 // pos, 是左子树还是右子树
 //@RTRN:返回当前插入的节点，其实就是node
 Node*    InsertNode( Node* root, Node* node, POS pos );
 void     Destroy();
 Node*    Root();
 
private:
 void     PreorderDump();
 void     InorderDump();
 void     PostOrderDump();
 
 void     Dump( METHOD method, String info );
 void     Output( String info );
 
 void     PreorderR( Node* node );
 void     InorderR( Node* node );
 void     PostorderR( Node* node );
 
private:
 Node*    m_pRoot;
};
 
#endif

BianryTreeImp.cpp 二叉树类的实现

#include "BinaryTree.h"
#include <vector>
 
// 使用vector实现了一个简单的堆栈，这里偷懒了，
// 使用链表会更快 
template <class T>
class Stack
{
public:
 void Push( const T& t ) { elements.insert( elements.begin(), t ); }
 T Pop() { T tmp = *(elements.begin());
         elements.erase( elements.begin() ); return tmp;  }
 bool IsEmpty() { return elements.empty(); }
 T Top() { return *(elements.begin()); }
 
private:
 std::vector<T> elements;
};
 
BinaryTree::BinaryTree(void)
{
 m_pRoot = NULL;
}
 
 
BinaryTree::~BinaryTree(void)
{
 Destroy();
}
 
void BinaryTree::CreateTree( const String& rootContent )
{
 if ( m_pRoot )
     Destroy();
 
 m_pRoot = new Node;
 m_pRoot->elem = rootContent;
}
 
// DESC: 这个函数是不完整的，缺少了对树的所有子节点的内存释放，
// 这里没写 
void BinaryTree::Destroy()
{
 if ( m_pRoot )
 {
     delete m_pRoot;
     m_pRoot = NULL;
 }
}
 
void BinaryTree::DumpTree( METHOD method, bool recursive )
{
 switch( method )
 {
 case Preorder:
     {
         if ( recursive )
         {
             PreorderR( m_pRoot );
             Output( "\n" );
         }
         else
         {
             PreorderDump();
         }
         break;
     }
 case Inorder:
     {
         if ( recursive )
         {
             InorderR( m_pRoot );
             Output( "\n" );
         }
         else
         {
             InorderDump();
         }
         break;
     }
 case Postorder:
     {
         if ( recursive )
         {
             PostorderR( m_pRoot );
             Output( "\n" );
         }
         else
         {
             PostOrderDump();
         }
         break;
     }
 }
}
 
void BinaryTree::PreorderDump()
{
 Node* p = m_pRoot;
 Stack<Node*> stack;
 while( p != NULL || !stack.IsEmpty() )
 {
     while ( p != NULL )
     {
         Output( p->elem );
         stack.Push( p );
         p = p->left;
     }
 
     if ( !stack.IsEmpty() )
     {
         p = stack.Pop();
         p = p->right;
     }
 }
 
 Output( "\n" );
}
 
void BinaryTree::InorderDump()
{
 Node* p = m_pRoot;
 Stack<Node*> stack;
 while( p != NULL || !stack.IsEmpty() )
 {
     if ( p != NULL )
     {
         stack.Push( p ); // if has left tree
         p = p->left;
     }
     else // left tree traversed
     {
         p = stack.Pop();
         Output( p->elem );
         p = p->right;
     }
 }
 
 Output( "\n" );
}
 
void BinaryTree::PostOrderDump()
{
 Node* p = m_pRoot;
 Stack<Node*> stack;
 Node* pPre = NULL;
 while( p != NULL || !stack.IsEmpty() )
 {
     if ( p != NULL )
     {
         stack.Push( p ); // if has left tree
         p = p->left;
     }
     else 
     {
         p = stack.Top();
         if ( p->right != NULL && pPre != p->right ) 
         {
             p = p->right;
         }
         else
         {
             p = pPre = stack.Top();
             Output( p->elem );
             stack.Pop();
             p = NULL;
         }
     }
 }
 
 Output( "\n" );
}
 
Node* BinaryTree::InsertNode( Node* root, Node* node, POS pos )
{
 switch ( pos )
 {
 case LeftChild:
     {
         root->left = node;
         break;
     }
 case RightChild:
     {
         root->right = node;
         break;
     }
 }
 
 return node;
}
 
Node* BinaryTree::Root()
{
 return m_pRoot;
}
 
void BinaryTree::Dump( METHOD method, String info )
{
 switch( method )
 {
 case Preorder:
     {
         printf( "Preorder: %s", info.data() );
         break;
     }
 case Inorder:
     {
         printf( "Inorder: %s", info.data() );
         break;
     }
 case Postorder:
     {
         printf( "Postorder: %s", info.data() );
         break;
     }
 }
}
 
void BinaryTree::Output( String info )
{
 printf( "%s", info.data() );
}
 
void BinaryTree::PreorderR( Node* node )
{
 if ( node )
 {
     // Visit
     Output( node->elem );
 
     PreorderR( node->left );
     PreorderR( node->right );
 }
}
 
void BinaryTree::InorderR( Node* node )
{
 if ( node )
 {
     InorderR( node->left );
 
     // Visit
     Output( node->elem );
 
     InorderR( node->right );
 }
}
 
void BinaryTree::PostorderR( Node* node )
{
 if ( node )
 {
     PostorderR( node->left );
     PostorderR( node->right );
 
     // Visit
     Output( node->elem );
 }
}

测试代码
树结构如下图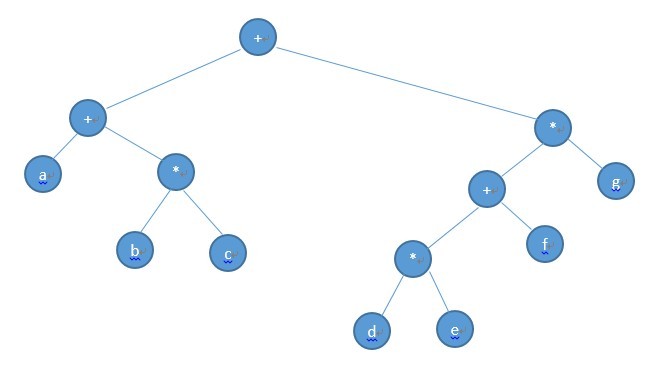
请输入图片描述

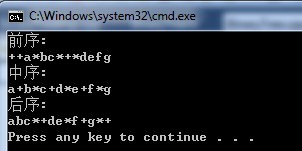
int _tmain(int argc, _TCHAR* argv[])
{
 BinaryTree* pTree = new BinaryTree;
 pTree->CreateTree( "+" );
 
 // Construct left child tree
 Node* pNow = pTree->InsertNode( pTree->Root(), new Node("+"), LeftChild );
 pTree->InsertNode( pNow, new Node("a"), LeftChild );
 pNow = pTree->InsertNode( pNow, new Node("*"), RightChild );
 pTree->InsertNode( pNow, new Node("b"), LeftChild );
 pTree->InsertNode( pNow, new Node("c"), RightChild );
 
 // Construct right child tree
 pNow = pTree->InsertNode( pTree->Root(), new Node("*"), RightChild );
 pTree->InsertNode( pNow, new Node("g"), RightChild );
 pNow = pTree->InsertNode( pNow, new Node("+"), LeftChild );
 pTree->InsertNode( pNow, new Node("f"), RightChild );
 pNow = pTree->InsertNode( pNow, new Node("*"), LeftChild );
 pTree->InsertNode( pNow, new Node("d"), LeftChild );
 pTree->InsertNode( pNow, new Node("e"), RightChild );
 
 printf( _T("前序:\n") );
 pTree->DumpTree( Preorder );
 printf( _T("中序:\n") );
 pTree->DumpTree( Inorder );
 printf( _T("后序:\n") );
 pTree->DumpTree( Postorder );
 
 delete pTree;
 pTree = NULL;
 return 0;
}

输出

本文由 BeijingJW 创作，采用知识共享署名4.0 国际许可协议进行许可
本站文章除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
最后编辑时间为: Jun 2, 2023 at 05:25 pm

二叉树的遍历 前序 中序 后序 分别实现递归和非递归遍历方式

二叉树的遍历前序中序后序分别实现递归和非递归遍历方式